srakacomputers.blogg.se - System of equations solver 3

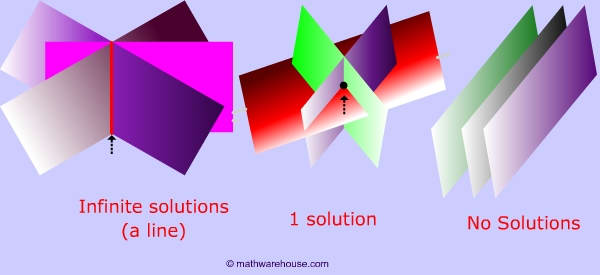
The second system has a single unique solution, namely the intersection of the two lines.

The first system has infinitely many solutions, namely all of the points on the blue line. The following pictures illustrate this trichotomy in the case of two variables: In the first case, the dimension of the solution set is, in general, equal to n − m, where n is the number of variables and m is the number of equations. Such a system is also known as an overdetermined system. In general, a system with more equations than unknowns has no solution.In general, a system with the same number of equations and unknowns has a single unique solution.Such a system is known as an underdetermined system. In general, a system with fewer equations than unknowns has infinitely many solutions, but it may have no solution.Here, "in general" means that a different behavior may occur for specific values of the coefficients of the equations. In general, the behavior of a linear system is determined by the relationship between the number of equations and the number of unknowns.

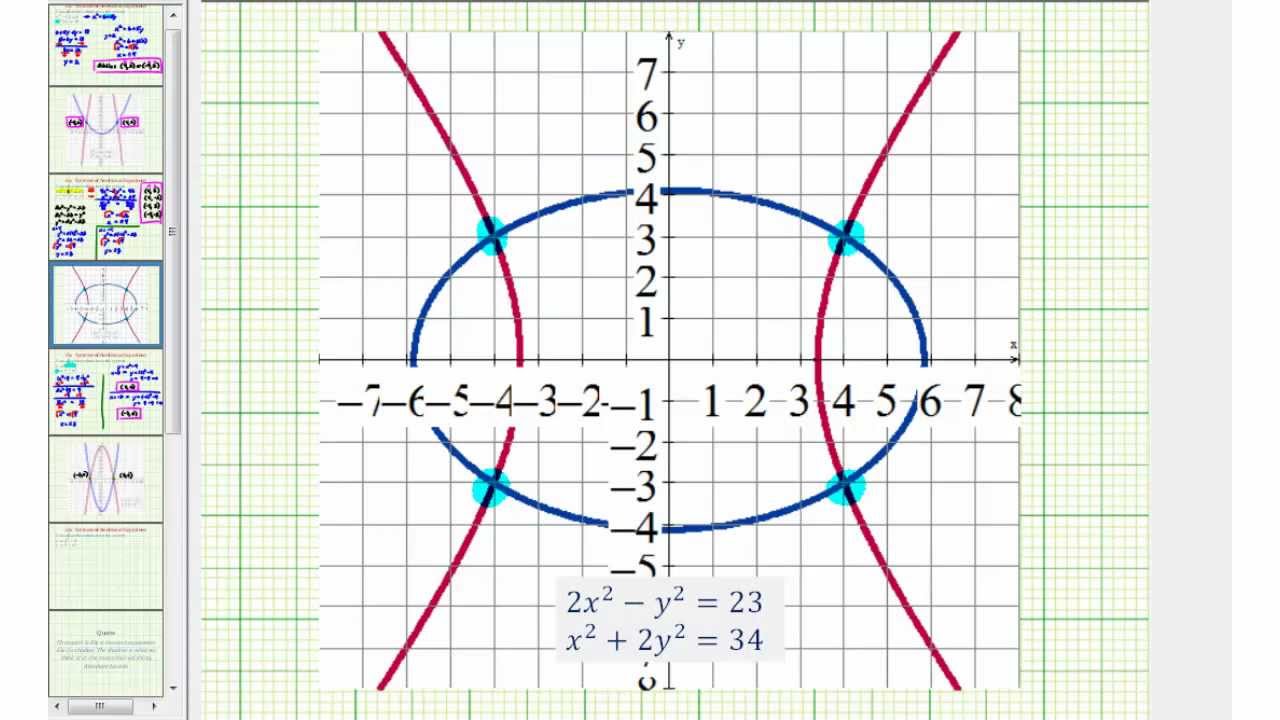
The solution set for two equations in three variables is, in general, a line. In systems of linear equations in three variables the desired solution is an ordered triple (x, y. The solution set is the intersection of these hyperplanes, and is a flat, which may have any dimension lower than n. 3.) No solution because the lines were parallel. įor n variables, each linear equation determines a hyperplane in n-dimensional space. For example, as three parallel planes do not have a common point, the solution set of their equations is empty the solution set of the equations of three planes intersecting at a point is single point if three planes pass through two points, their equations have at least two common solutions in fact the solution set is infinite and consists in all the line passing through these points. Thus the solution set may be a plane, a line, a single point, or the empty set. Because a solution to a linear system must satisfy all of the equations, the solution set is the intersection of these lines, and is hence either a line, a single point, or the empty set.įor three variables, each linear equation determines a plane in three-dimensional space, and the solution set is the intersection of these planes. You can enter your linear equation into Wolfram Alpha and get a symbolic solution. Since your matrix is block diagonal, so is your solution.

The system has a single unique solution.įor a system involving two variables ( x and y), each linear equation determines a line on the xy- plane. Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Pi (Product) Notation Induction Logical Sets Word Problems. Here is the right-hand-side vector: (source: ) You solve this system of equations by solving.

The system has infinitely many solutions.

The set of all possible solutions is called the solution set.Ī linear system may behave in any one of three possible ways: , x n such that each of the equations is satisfied. The solution set for the equations x − y = −1 and 3 x + y = 9 is the single point (2, 3).Ī solution of a linear system is an assignment of values to the variables x 1, x 2. The number of vectors in a basis for the span is now expressed as the rank of the matrix. Since one equation has no S variable, it may be helpful to use the other two equations and eliminate the S variable from them. Multiply both sides of the second equation by −10.A linear system in three variables determines a collection of planes The intersection point is the solution. Step 1: First choose two equations and eliminate a variable. A solution to a system of three equations in three variables \left(x,y,z\right),\text

In order to solve systems of equations in three variables, known as three-by-three systems, the primary goal is to eliminate one variable at a time to achieve back-substitution. Write the equations for a system given a scenario, and solve.Use back substitution to find a solution to a system of three equations.Determine whether an ordered triple is a solution to a system of three equations.